Faizal: Wheatstone bridge (Jembatan Wheatstone)

Jembatan Wheatstone adalah rangkaian listrik yang digunakan untuk mengukur hambatan listrik yang tidak diketahui dengan menyeimbangkan dua kaki rangkaian jembatan , yang salah satu kakinya mencakup komponen yang tidak diketahui. Manfaat utama dari rangkaian ini adalah kemampuannya untuk memberikan pengukuran yang sangat akurat (berbeda dengan pembagi tegangan sederhana ). ^[1] Pengoperasiannya mirip dengan potensiometer asli .

Jembatan Wheatstone ditemukan oleh Samuel Hunter Christie (terkadang dieja "Christy") pada tahun 1833 dan diperbaiki serta dipopulerkan oleh Sir Charles Wheatstone pada tahun 1843. Salah satu kegunaan awal jembatan Wheatstone adalah untuk analisis dan perbandingan tanah . ^[2]

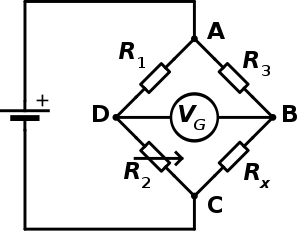
Pada gambar, $R x$ adalah resistansi tetap yang harus diukur, namun belum diketahui.

$R 1$ , $R 2$ ,dan $R 3$ adalah resistor yang resistansinya diketahui dan resistansi $R 2$ dapat disesuaikan. Resistansi $R 2$ diatur sampai jembatan “seimbang” dan tidak ada arus yang mengalir melalui galvanometer $V g$ . Pada titik ini,beda potensialantara dua titik tengah (BdanD) akan menjadi nol. Oleh karena itu perbandingan kedua hambatan pada bagian yang diketahui $(R 2 / R 1)$ sama dengan perbandingan kedua hambatan pada bagian yang tidak diketahui $(R x / R 3)$ . $Jika jembatan tidak seimbang ,$ arah arus menunjukkan apakah $R2$ terlalu tinggi atau terlalu rendah.

Pada titik keseimbangan,

{\begin{aligned}{\frac {R_{2}}{R_{1}}}&={\frac {R_{x}}{R_{3}}}\\[4pt]\Rightarrow R_{x}&={\frac {R_{2}}{R_{1}}}\cdot R_{3}\end{aligned}}

Mendeteksi arus nol dengan galvanometer dapat dilakukan dengan presisi yang sangat tinggi. Oleh karena itu, jika $R 1$ , $R 2$ , dan $R 3$ diketahui memiliki presisi tinggi, maka $R x$ dapat diukur dengan presisi tinggi. Perubahan yang sangat kecil pada $R x$ mengganggu keseimbangan dan mudah dideteksi.

Alternatifnya, jika $R 1$ , $R 2$ , dan $R 3$ diketahui, tetapi $R 2$ tidak dapat disesuaikan, perbedaan tegangan atau arus yang mengalir melalui meteran dapat digunakan untuk menghitung nilai $R x$ , menggunakan hukum rangkaian Kirchhoff . Pengaturan ini sering digunakan dalam pengukur regangan dan pengukuran termometer resistansi , karena biasanya lebih cepat membaca level tegangan dari satu meter daripada menyesuaikan resistansi ke tegangan nol.

Derivasi cepat dengan keseimbanganSunting

Pada titik keseimbangan, tegangan dan arus antara dua titik tengah ( B dan D ) adalah nol. Karena itu, $I_{1}=I_{2}$ , $I_{3}=I_{x}$ , $V_{D}=V_{B}$ .

Karena $V_{D}=V_{B}$ , itu berdiri $V_{DC}=V_{BC}$ Dan $V_{AD}=V_{AB}$ .

Membagi dua persamaan terakhir dengan anggota dan menggunakan persamaan arus di atas, diperoleh:

${\begin{aligned}{\frac {V_{DC}}{V_{AD}}}&={\frac {V_{BC}}{V_{AB}}}\\[4pt]\Rightarrow {\frac {I_{2}R_{2}}{I_{1}R_{1}}}&={\frac {I_{x}R_{x}}{I_{3}R_{3}}}\\[4pt]\Rightarrow R_{x}&={\frac {R_{2}}{R_{1}}}\cdot R_{3}\end{aligned}}$

Derivasi penuh menggunakan hukum rangkaian KirchhoffSunting

Pertama, hukum pertama Kirchhoff digunakan untuk mencari arus pada persimpangan B dan D :

{\begin{aligned}I_{3}-I_{x}+I_{G}&=0\\I_{1}-I_{2}-I_{G}&=0\end{aligned}}

Kemudian, hukum kedua Kirchhoff digunakan untuk mencari tegangan pada loop ABDA dan BCDB :

{\begin{aligned}(I_{3}\cdot R_{3})-(I_{G}\cdot R_{G})-(I_{1}\cdot R_{1})&=0\\(I_{x}\cdot R_{x})-(I_{2}\cdot R_{2})+(I_{G}\cdot R_{G})&=0\end{aligned}}

Jika jembatan seimbang, maka $I G = 0$ , sehingga persamaan himpunan kedua dapat ditulis ulang menjadi:

{\begin{aligned}I_{3}\cdot R_{3}&=I_{1}\cdot R_{1}\quad {\text{(1)}}\\I_{x}\cdot R_{x}&=I_{2}\cdot R_{2}\quad {\text{(2)}}\end{aligned}}

Kemudian persamaan (1) dibagi dengan persamaan (2) dan persamaan yang dihasilkan disusun ulang sehingga menghasilkan:

R_{x}={{R_{2}\cdot I_{2}\cdot I_{3}\cdot R_{3}} \over {R_{1}\cdot I_{1}\cdot I_{x}}}

Karena $I 3 = I x$ dan $I 1 = I 2$ sebanding dengan Hukum Pertama Kirchhoff, maka $I 3 I 2 / I 1 I x$ menghilangkan persamaan di atas. Nilai $R x$ yang diinginkan sekarang diketahui diberikan sebagai:

R_{x}={{R_{3}\cdot R_{2}} \over {R_{1}}}

Sebaliknya, jika resistansi galvanometer cukup tinggi sehingga $I G$ dapat diabaikan, maka dimungkinkan untuk menghitung $R x$ dari ketiga nilai resistor lainnya dan tegangan suplai ( $V S$ ), atau tegangan suplai dari keempat resistor tersebut. nilai-nilai. Untuk melakukannya, kita harus menghitung tegangan dari masing-masing pembagi potensial dan mengurangkan tegangan yang satu dengan yang lain. Persamaan untuk ini adalah:

{\begin{aligned}V_{G}&=\left({R_{2} \over {R_{1}+R_{2}}}-{R_{x} \over {R_{x}+R_{3}}}\right)V_{s}\\[6pt]R_{x}&={{R_{2}\cdot V_{s}-(R_{1}+R_{2})\cdot V_{G}} \over {R_{1}\cdot V_{s}+(R_{1}+R_{2})\cdot V_{G}}}R_{3}\end{aligned}}

dimana $V G$ adalah tegangan node D relatif terhadap node B.

jadi Jembatan Wheatstone menggambarkan konsep pengukuran perbedaan, yang bisa sangat akurat. Variasi pada jembatan Wheatstone dapat digunakan untuk mengukur kapasitansi , induktansi , impedansi , dan besaran lainnya, seperti jumlah gas yang mudah terbakar dalam sampel, dengan alat peledak . Jembatan Kelvin secara khusus diadaptasi dari jembatan Wheatstone untuk mengukur resistansi yang sangat rendah. Dalam banyak kasus, pentingnya mengukur resistansi yang tidak diketahui terkait dengan pengukuran dampak beberapa fenomena fisik (seperti gaya, suhu, tekanan, dll.) sehingga memungkinkan penggunaan jembatan Wheatstone dalam mengukur elemen-elemen tersebut secara tidak langsung.

Reference:

"Circuits in Practice: The Wheatstone Bridge, What It Does, and Why It Matters", as discussed in this MIT ES.333 class video
^ "The Genesis of the Wheatstone Bridge" by Stig Ekelof discusses Christie's and Wheatstone's contributions, and why the bridge carries Wheatstone's name. Published in "Engineering Science and Education Journal", volume 10, no 1, February 2001, pages 37–40.
https://en.m.wikipedia.org/wiki/Wheatstone_bridge